08/11/2022
La resta de vectores es una operación fundamental en álgebra vectorial con diversas aplicaciones en física, ingeniería y otras áreas. A diferencia de la suma, que se realiza uniendo los vectores, la resta implica encontrar la diferencia entre dos vectores. Comprender cómo graficar la resta de vectores es crucial para visualizar y resolver problemas.
Métodos para graficar la resta de vectores
Existen dos métodos principales para graficar la resta de vectores: el método gráfico y el método analítico (usando componentes).
Método Gráfico:
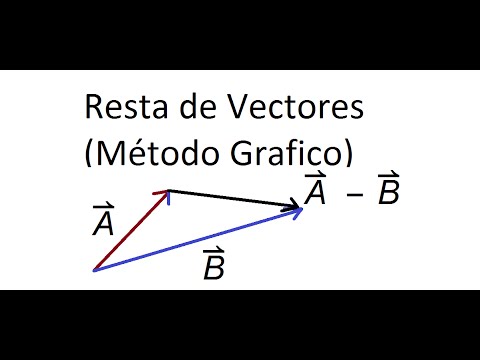
Este método se basa en la representación visual de los vectores. Para restar un vector b de un vector a ( a - b ), seguimos estos pasos:
- Dibujar los vectores: Representar gráficamente ambos vectores, a y b , con su origen en el mismo punto. Es importante mantener la escala y la dirección correctas.
- Trasladar el vector b: Trasladar el vector b de forma que su origen coincida con la punta del vector a . Mantener la magnitud y la dirección del vector b inalteradas durante el traslado.
- Dibujar el vector resultante: Dibujar un vector desde el origen del vector a hasta la punta del vector b (trasladado). Este nuevo vector representa la resta a - b . La magnitud y la dirección de este vector representan la magnitud y la dirección de la diferencia entre los dos vectores originales.
Ejemplo:
Imaginemos dos vectores: a con magnitud 5 unidades y dirección 30 grados respecto al eje x, y b con magnitud 3 unidades y dirección 120 grados respecto al eje x. Para graficar a - b, primero dibujamos ambos vectores con origen común. Luego, trasladamos b para que su origen coincida con la punta de a. Finalmente, el vector que une el origen de a con la punta del vector b trasladado representa la resta a - b.
Método Analítico (Componentes):
Este método se basa en descomponer los vectores en sus componentes y realizar la resta componente a componente. Si a = (a x, a y) y b = (b x, b y), entonces la resta a - b se calcula como:
a - b = (a x- b x, a y- b y)
Una vez calculadas las componentes del vector resultante, podemos graficar el vector utilizando estas componentes. El vector resultante tendrá su origen en el origen de coordenadas (0,0) y su punta en el punto (a x- b x, a y- b y).
Ejemplo:
Si a = (4, 3) y b = (1, 2), entonces:
a - b = (4 - 1, 3 - 2) = (3, 1)

Para graficar este vector, ubicamos el punto (3, 1) en el plano cartesiano y dibujamos un vector desde el origen (0,0) hasta este punto.
Comparación de Métodos:
| Método | Ventajas | Desventajas |
|---|---|---|
| Método Gráfico | Visualización directa del resultado. Fácil de entender conceptualmente. | Puede ser menos preciso que el método analítico, especialmente con vectores de magnitudes o ángulos complejos. Depende de la precisión del dibujo. |
| Método Analítico | Mayor precisión. Aplicable a vectores en cualquier número de dimensiones. Permite cálculos más complejos. | Requiere conocimientos de trigonometría y álgebra vectorial. Puede ser menos intuitivo para principiantes. |
Consultas Habituales:
- ¿Cómo se resta un vector de sí mismo? Al restar un vector de sí mismo, el resultado es siempre el vector nulo (un vector con magnitud cero).
- ¿Qué sucede si resto dos vectores con la misma magnitud pero direcciones opuestas? El vector resultante tendrá el doble de la magnitud de cada vector original, y su dirección coincidirá con la dirección del vector que se está restando.
- ¿Puedo restar vectores en tres dimensiones? Sí, el método analítico se extiende fácilmente a tres o más dimensiones. Simplemente se restan las componentes correspondientes en cada dimensión.
- ¿Es conmutativa la resta vectorial? No, la resta vectorial no es conmutativa. a - b no es igual a b - a .
Aplicaciones de la Resta de Vectores:
La resta de vectores tiene una amplia gama de aplicaciones en diversos campos:
- Física: Cálculo de la velocidad relativa entre dos objetos, determinación de la fuerza resultante de varias fuerzas actuando sobre un objeto.
- Ingeniería: Análisis de estructuras, diseño de mecanismos, simulación de sistemas.
- Gráficos por computadora: Transformaciones geométricas, iluminación y sombreado.
- Navegación: Determinación de la posición relativa de un objeto.
Comprender cómo graficar la resta de vectores es fundamental para resolver problemas en diferentes áreas. El método gráfico proporciona una visualización intuitiva, mientras que el método analítico ofrece mayor precisión y se extiende a problemas más complejos. La elección del método dependerá de la complejidad del problema y de las herramientas disponibles.
Ejercicios de Práctica:
Para consolidar su comprensión, practique con los siguientes ejemplos:
- Reste los vectores a = (2, 5) y b = (1, 3) usando ambos métodos (gráfico y analítico). Compare sus resultados.
- Grafique la resta de dos vectores con magnitudes iguales pero direcciones opuestas.
- Reste el vector a = (4, 2, -1) del vector b = (1, -3, 2).
Resolver estos ejercicios le ayudará a dominar la resta de vectores y a aplicar estos conceptos en problemas más complejos. Recuerde que la práctica constante es clave para el dominio de cualquier concepto matemático.

